Euclides - Los Elementos (Libro II: Cuadrados y rectángulos)

Habíamos visto en el libro precedente, las 48 proposiciones que se basan en los 5 postulados clásicos de Euclides. Esta vez veremos algo similar, pero con respecto a las áreas de los cuadrados y rectángulos. Otra diferencia que podremos ver en este libro es que las proposiciones se reducen a sólo 18 de ellas, por lo que este libro será aún más corto que el anterior. Las proposiciones de Euclides tendrán una gran influencia y contribución en las demás ciencias como la física, astronomía, matemáticas y otras.

Otros libros de Euclides:

Libro I: Triángulos
Libro III: Circunferencias

LOS ELEMENTOS

LIBRO II: CUADRADOS Y RECTÁNGULOS

Conceptos básicos

Gnomon: El gnomon es el resultado de remover la esquina de un paralelogramo más grande, siendo el más grande el gnomon. En este caso, el gnomon se encontraría de la siguiente forma.

Proposiciones

Proposición 1:

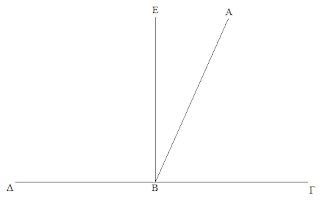
Si hay dos rectas y una de ellas se corta en un número cualquiera de segmentos, el rectángulo comprendido por las dos rectas es igual a los rectángulos comprendidos por la recta no cortada y cada uno de los segmentos

Tengamos dos rectas: una recta A y una recta BΓ y córtese esta última en un punto Δ y E. 

Luego prolonguemos B hasta el punto Z para que se forme un ángulo recto con BΓ. Luego indiquese un punto H entre la recta BΓ que sería igual a la recta A, es decir BH es igual a A.

De la misma forma, a partir de H extiendase la recta hasta el punto Θ hasta Γ. Por los puntos  Δ, Γ y E tracese una recta que los una en la recta HΘ. Finalmente, unase Δ con una recta K, E con una recta Λ. 

Ahora téngase en cuenta que BΘ es igual a los rectángulos BK, ΔΛ y EΘ que en realidad, son la suma del rectángulo BΘ. De la misma forma, BH, ΔK, EΛ y ΓΔ son iguales a BH que a su vez es igual a A. 

También podemos ver que BΓ es la suma de los rectángulos BΔ, BE y EΓ, y a su vez estos mismos están contenidos en la recta A porque BΓ es igual a BH. 

Finalmente, Así se llevaría la distribución de rectángulos en la recta A:

BK estaría en el rectángulo comprendido por A, que sería BΔ.
ΔΛ estaría en el rectángulo comprendido por A, que sería ΔE.
EΘ estaría en el rectángulo comprendido por A, que sería EΓ.

Así, los rectángulos comprendidos por la recta no cortada, serán iguales a los rectángulos comprendidos por la recta que sí se cortó. 

Proposición 2:

Si se corta al azar una línea recta, el rectángulo comprendido por la recta entera y cada uno de los segmentos es igual al cuadrado de la recta entera. 

Tengamos una recta AB que se corte por un punto Γ. 

Dice Euclides que AB está comprendido por los rectángulos BΓ, BA y AΓ. 

Luego, a partir de AB hágase el cuadrado AΔEB y luego tracese por Γ la recta ΓZ. 

Euclides dice que los rectángulos AZ y ΓE comprenden la totalidad de AB. 

AE es igual a AZ y ΓE, ya que el rectángulo AE está comprendido por las rectas AΔ y AΓ, pero como AΔEB es un cuadrado, AD y AB serán iguales.

Del mismo modo, AΔ es igual a AB al igual que ΓE, ya que los dos están comprendidos en AB. Si AΔ es igual a AB, de la misma forma BE es igual a AΔ,y así tenemos que AΔ y BE son iguales a AB.

Como conclusión, se demuestra que al trazar una recta (AB) sobre un punto cualquiera (Γ), el rectángulo comprendido por cada uno de los segmentos (AΓ y ΓB) es igual al cuadrado de la recta entera AB (AΔEB).

Proposición 3:

Si se corta al azar una línea recta, el rectángulo comprendido por la recta entera y uno de los segmentos es igual al rectángulo comprendido por los segmentos y el cuadrado del segmento primeramente dicho

Nuevamente cortemos una recta AB en un punto Γ. 

Ahora, a partir de la recta ΓB formamos el triángulo ΓΔEB.

Luego debemos prolongar EΔ hasta Z para formar un rectángulo completo AZEB.

De aquí podemos decir que AE es igual a AΔ junto con el cuadrado BΓ.

Bajo este respecto, recordemos que AE es el rectángulo comprendido por AΓ y por BΓ.

También deberemos decir que ΔΓ es igual a BΓ ya que es parte del cuadrado ΓΔEB. 

Así, si se corta al azar una línea recta (AB)en un punto cualquiera (Γ) el rectángulo comprendido por la recta entera y uno de los segmentos es igual al rectángulo comprendido (AZΔΓ) por los segmentos y el cuadrado del segmento primeramente dicho. 

Proposición 4:

Si se corta al azar una línea recta, el cuadrado de la recta entera es igual a los cuadrados de los segmentos y dos veces el rectángulo comprendido por los segmentos

Otra vez tenemos la misma recta AB cortada por un punto Γ, pero esta vez lo haremos en otra parte.

A partir de esta recta debemos construir el cuadrado AΔEB, mientras que del punto Γ prolongar un punto Z para conformar la recta ΓZ.

Luego entre ΓZ poner un punto H para formar las rectas paralelas ΘK que serán paralelas a AB y a ΔE. Después de esto debemos trazar una recta en diagonal uniendo BΔ. 

También deberíamos decir que ΓZ es paralela a AΔ y BE, y BΔ ha incidido sobre ellas.  

Al suceder esto, tenemo que el ángulo ΓHB es igual al ángulo interno y opuesto AΔB. Ahora, el ángulo AΔB es igual al ángulo ABΔ porque BA es igual al lado AΔ. 

Del mismo modo, ΓHB es igual al ángulo HBΓ, porque BΓ es igual al lado ΓH. Por otro lado, también tenemos que ΓB es igual a HK y ΓH a KB; lo que da como resultado que ΓHKB sea un cuadrado equilátero. 

¿ΓHKB es un rectángulo o un cuadrado?

Euclides dice que ΓHKB también es rectangular debido a que ΓH es paralela a BK. Así, los ángulos KBΓ y HΓB son iguales a dos rectos, pero también se ha dicho que son equilateros ¿cuál de las dos figuras será? ΓHKB será mucho más cuadrado que rectángulo porque cumple con las dos condiciones de ser un cuadrado:

Cuadrado: figura equilátera con cuatro ángulos rectos
Rectángulo: figura con cuatro ángulos rectos. 

Si bien ΓHKB tiene ángulos rectos (por lo que cumpliría ser un rectángulo) sus lados equiláteros hacen que cumpla con las propiedades de un cuadrado. 

De la misma forma, ΘZ también sería un cuadrado y es el cuadrado de ΘH.

Por lo tanto, si se corta al azar una línea recta (AB), el cuadrado de la recta entera (ADEB) es igual a los cuadrados de los segmentos y dos veces el rectángulo comprendido por los segmentos. 

Proposición 5:

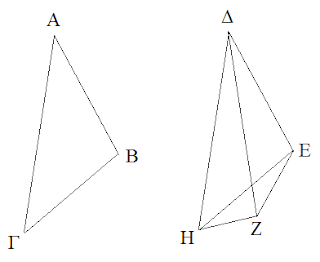
Si se corta una línea recta en segmentos iguales y desiguales, el rectángulo comprendido por los segmentos desiguales de la recta entera junto con el cuadrado de la recta que está entre los puntos de sección, es igual al cuadrado de la mitad

Tengamos una recta AB con segmentos iguales en el punto Γ y un segmento desigual en el punto Δ. 

Luego construir a partir de ΓB un cuadrado ΓEZB y trazar EB por el punto Δ. Después por el punto Δ una recta ΔH que incida en la recta EB y forme el punto Θ. 

Posteriormente trazar una línea KM que sea paralela tanto a AB como a EZ. Este a su vez formará el punto Λ que coincidirá con Γ y formará la recta ΓΛ. 

Teniendo este cuadro, podremos decir que ΓΘ es igual a ΘZ (proposición 43 del primer libro), de la misma forma que ΓM es igual a AΛ, porque AΓ es igual a ΓB.

También podremos decir que AΛ es igual a ΔZ porque ésta última es igual a ΓM. Luego, a estos dos rectángulos se debe añadir ΓΘ para formar el rectángulo AΘ. 

Bajo este respecto, podemos decir que si a AΛ le añadimos ΓΘ, entonces esta sería igual que el rectángulo ΔZ y ΓΘ unidos. De hecho, esta combinación formaría lo que se conoce como el gnomon. 

El gnomon es el resultado de remover la esquina de un paralelogramo más grande, siendo el más grande el gnomon. En este caso, el gnomon se encontraría de la siguiente forma.

A partir de esto se formarían los puntos MNΞ que representarían el gnomon en el rectángulo. 

Por lo tanto, si se corta una línea recta (AB) en segmentos iguales (AΓ y ΓB) y desiguales (AΔ y ΔB), juntos con el cuadrado de a recta que está entre los puntos de sección (ΓΔ) es igual al cuadrado de la mitad de la recta. 


Proposición 6:

Si se divide en dos partes iguales una línea recta y se le añade, en línea recta, otra recta, el rectángulo comprendido por la recta entera con la recta añadida y la recta añadida junto con el cuadrado de la mitad es igual al cuadrado de la recta compuesta por la mitad y la recta añadida

Tengamos una recta AB con un punto intermedio Γ, y prolongar B hasta un punto Δ. 

A partir de ΓΔ construyase el cuadrado ΓEZΔ y tracese ΔE mientras que por el punto B debe formarse la recta BH.

Luego, por el punto BH donde incide ΔE debe colocarse el punto Θ, y en este trazar la recta KM junto para que sea paralelas con AB y EZ. De este modo también se formará el punto Λ y unir A con K.

De esta forma, AΛ es igual a ΓΘ, así como este rectángulo es igual a ΘZ. 

El rectángulo entero AM es igual al gnomon que se forma en NΞO como veremos a continuación. 

Como AM es igual a NΞO, entonces AM junto con AH son iguales al cuadrado ΓΔ que es lo que se quería demostrar. 

El rectángulo comprendido por la recta entera y la recta añadida (AB y BΔ) junto con el cuadrado originado a partir de la mitad de la recta entera, el cuadrado de ΓB será igual al cuadrado de la recta entera junto con la recta añadida (ΓΔ).

Proposición 7:

Si se corta al azar una línea recta, el cuadrado de la recta entera y el de uno de los segmentos tomados conjuntamente son iguales a dos veces el rectángulo comprendido por la recta entera y el segmento antedicho más el cuadrado del segmento restante

Cortar al azar un punto Γ en la recta AB. 

A partir de AB se debe construir AΔEB y construir la recta ΓN. Luego se debe trazar la recta BΔ para que junto con la recta ΓN se forme el punto H y la recta ΘZ.

En este caso, AZ es igual a ΓE y si unimos estos dos rectángulos también podríamos decir que estos dos forman un gnomon KΛM.

De esta forma, ΓZ y el gnomon KΛM son el doble que el rectángulo entero de AZ. Ahora, si queremos completar el cuadrado completo, deberemos sumar el gnomon KΛM con el cuadrado HΔ. 

Finalmente, así se conforma el cuadro AΔEB que son la suma del gnomon y del cuadrado HΔ.

Proposición 8:

Si se corta al azar una línea recta, cuatro veces el rectángulo comprendido por la recta entera y uno de los segmentos junto con el cuadrado del segmento restante es igual al cuadrado construido a partir de la recta entera y del segmento primeramente dicho, tomados como una sola recta

Cortar al azar la recta AB en un punto Γ y luego se debe prolongar B hasta Δ en la misma línea AB.

BΔ es igual a ΓB y se construye a partir de AΔ. Luego, a partir de AΔ se debe construir el cuadrado AEZΔ.

Ahora deberemos construir la recta ΓΔ y BΛ, para luego unir Δ con E por medio de una recta.

Después, como ΔE incide en las rectas ΓΔ y BΛ, entonces deberemos formar dos rectas (MN y ΞO) entre las rectas verticales. 

Con todos estos puntos externos deberemos apuntar aquellos que se intersectan los unos con los otros de la siguiente manera. 

De esta forma ΓB y BΔ son iguales, así como también ΓB es igual a HK, ΠP y ΔΛ que son todas paralelas. De la misma forma BΔ es igual a KN, PO y ΛZ. 

Luego ΓK es igual a PN como MΠ es igual a ΠΛ, y este al rectángulo PZ. Por otro lado, ΓK, HP, PN y KΔ son el cuádruple de ΓK. 

Así, se conforma un gnomon que comprende AN y ΓZ juntos. Para indicar el gnomon más precisamente añadiremos los puntos ΣTY.

El gnomon ΣTY son el cuádruple de AK y por lo tanto cuatro veces el rectángulo AB y BΔ. 

Como conclusión, se demuestra que el cuádruple del triángulo formado a partir de la recta entera junto a otro segmento (AK) más el cuadrado del segmento restante (ΞΘ) es igual al cuadrado de la recta inicial junto al segmento añadido (AZ).

Proposición 9:

Si se corta una línea recta en partes iguales y desiguales, los cuadrados de los segmentos desiguales de la recta entera son el doble del cuadrado de la mitad más el cuadrado de la recta situada entre los puntos de sección

Cortese AB en segmentos iguales por el punto Γ, y en desiguales por el punto Δ. 

Ahora deberemos trazar por Γ una recta E y formar ΓE, para luego unir EA y EB. Por el punto Δ deberemos unir un punto Z para crear ΔZ . Luego debemos crear una línea paralela para crear ZH que intersecta con la recta ΓE. Finalmente tracese AZ.

AΓ es igual a ΓE y el ángulo EAΓ y AEΓ son iguales a un recto, así como también ΓEA y ΓAE son la mitad de un recto. 

Por otro lado, ΓEB y ΓBE son también la mitad de un recto y así el ángulo AEB entero es un ángulo recto. 

Luego como HEZ es la mitad de un recto y el ángulo EHZ es recto, entonces el ángulo HZE es también la mitad de un recto. De la misma forma, ZΔB también es un ángulo recto y BZΔ es la mitad de un recto. 

A partir de esto, podríamos decir también que el cuadrado de EA es el doble que AΓ, así como también EZ es el doble de EH. 

Finalmente, el rectángulo AΔ y BΔ son el doble de AΓ y ΓΔ. 

Como conclusión, como EA es el doble de AΓ, ya que AΓ es igual a ΓE, y lo mismo pasa con EZ. Luego, como HZ es igual a ΓΔ y EH es igual a HZ. Así, EZ es el doble de ΓΔ. 

AE junto con EZ es igual al doble de AΓ junto con el doble de ΓΔ. Por otro lado, AZ es igual a los cuadrados AE y EZ. 

Como los cuadrados AΔ y ΔZ son iguales al cuadrado de AZ, y entonces AΔ junto con ΔZ es igual al doble de AΓ y el doble de ΓΔ que es lo que se quería demostrar.

Proposición 10:

Si se divide en dos partes iguales una línea recta y se le añade, en línea recta, otra recta, el cuadrado de la recta entera con la recta añadida y el cuadrado de la añadida, tomados conjuntamente son el doble del cuadrado de la mitad y el cuadrado construido a partir de la recta compuesta por la mitad y la recta añadida, tomadas como una sola recta

Tengamos una recta AB trazada por un punto Γ. haciendo que AB y AΓ sean iguales, y luego debe prolongarse B hasta el punto Δ.

Similarmente a la proposición 9 ser debe hacer una recta a partir de Γ para formar ΓE, y unase AB con E. 

Y por E se debe trazar el punto Z para que se una con Δ. Ya que tenemos ZΔ, en esta misma recta debemos prolongar la misma hasta el punto H, para luego unir A y E con H. 

AΓ es igual a ΓE porque ΓE es igual a ΓB y por esto el ángulo EAΓ es igual a AEΓ, y en la intersección AΓ y ΓB se forma un ángulo recto.

ΓEB y EBΓ son la mitad de un recto (cada uno) porque EAΓ y AEΓ son iguales a la mitad de un recto también, y por lo tanto AEB comprende un ángulo recto. Y como EBΓ es la mitad de un recto, entonces ΔBH es también la mitad de un recto. 

El ángulo BΔH es un ángulo recto porque es igual al ángulo ΔΓE y por otro lado, ΔHB sería la mitad de un recto y es igual al ángulo ΔBH. 

ZEH es la mitad de un recto al igual que EHZ desde que HZ es igual a EZ. 

EΓ es igual a ΓA y la unión de estos dos son el doble a ΓA, y EA es el doble del cuadrado ΓE y ΓA. 

ZΔ es igual a EZ y la unión de estos son el doble de EZ, y EH es el doble del cuadrado EZ. 

EZ es igual a ΓΔ y EH es el doble de ΓΔ porque éste es igual a EZ Y EH es el doble de ΓΔ porque es el doble de EZ. Por otro lado, recordemos también que EA es el doble de AΓ. Por lo tanto, AE y EH son el doble de AΓ y ΓΔ. Así mismo, también AH es igual al cuadrado de AΔ y EH.

EA es el doble de AΓ, y EH es el doble de ΓΔ, entonces AH será igual al doble de AΓ y el doble de ΓΔ.

Los cuadrados de AΔ y ΔH son iguales al cuadrado de AH, y así los cuadrados de AΔ y ΔH son el doble de los cuadrados AΓ y ΓΔ. 

Finalmente, si a una recta se le agregara otra recta siguiendo la misma línea el cuadrado de la recta inicial con la añadida junto con el cuadrado de la recta agregada, será igual al doble de la mitad de la recta original junto con el doble de la mitad de la recta inicial unida a la recta añadida. 

Proposición 11:

Dividir una recta dada de manera que el rectángulo comprendido por la recta entera y uno de los segmentos sea igual al cuadrado del segmento restante

Tengamos AB como una recta dada y a partir de esta se construya el cuadrado ABΔΓ. 

Luego dividamos AΓ por el punto E y luego unir este punto con B para formar la recta EB. Después se debe prolongar ΓA hasta Z, para que ZE sea igual que EB. 

Posteriormente, a partir de AZ fórmese el cuadrado ZHΘA, y Θ debe unirse con el punto K. 

El rectángulo comprendido por ΓZ y ZA junto con el cuadrado de AE es igual al cuadrado de EZ. 

Y si EZ es igual a EB, el rectángulo comprendido por ΓZ y ZA junto con el cuadrado AE es igual al cuadrado EB y también a los cuadrados BA, AE. 

Ahora quitemos de ambos lados el cuadrado AE. Su resultado será que ΓZ y ZA serán iguales al cuadrado de AB.

Luego, el rectángulo comprendido por ΓZ y ZA es ZK porque AZ es igual a ZH, pero el cuadrado de AB es AΔ, por lo tanto, ZK es igual a AΔ. 

Quitemos de ambos (ZK y AΔ) el rectángulo AK y entonces el cuadrado restante de ZK será ZΘ y de AΔ será ΘΔ.  Así como este último (ΘA) es el rectángulo comprendido por AB y BΘ; porque AB es igual a BΔ. Así, AB y BΘ es iguala la cuadrado de ΘΔ.

Como conclusión, la recta dada (AB) ha sido dividida en un punto (Θ) de manera tal que el rectángulo comprendido por AB y BΘ sea igual al cuadrado AΘ.

Proposición 12:

En los triángulos obtusángulos el cuadrado del lado que subtiende al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso

Sea ABΓ el triángulo obtusángulo que tiene el ángulo obtuso BAΓ. 

Y a partir del punto B tracese Δ para formar la recta BΔ.

Lo que se quiere demostrar aquí es que el cuadrado de BΓ es mayor dos veces mayor el rectángulo comprendido por ΓA y ΔA a los cuadrados AΓ y AB. 

Así, podríamos decir que BΓ es igual al doble de ΓA, ΔA, y AΓ y AB juntos.

¿Cómo se demuestra? calculando el triángulo de ΔBΓ que posee un ángulo recto en Δ.

Por otro lado, ΓΔ es igual al cuadrado de AΓ y AΔ junto con el doble del rectángulo ΓA y ΔA. 

Ahora para demostrar que BΓ es mayor que el doble de AΓ, AB, y el doble que ΓA y ΔA se propone hacer que ΔB esté en ambos lados de la ecuación propuesta por Euclides: ΔΓ = ΓA + AΔ + 2 (AΓ, AΔ)

BΓ = (ΓΔ + ΔB)
AB = AΔ + ΔB

Por lo tanto, podríamos expresar lo siguiente:

ΓΔ + ΔB = AΓ + (AΔ + ΔB) + 2 veces ΓA y AΔ

Todo esto se puede reemplazar finalmente por la siguiente expresión:

BΓ = AΓ + AB + 2 veces ΓA y AΔ.


Proposición 13:

En los triángulos acutángulos, el cuadrado del lado que subtiende al ángulo agudo es menor que los cuadrados de los lados que comprenden el ángulo agudo en dos veces el rectángulo comprendido por uno de los lados del ángulo agudo sobre el que cae la perpendicular y la recta interior cortada por la perpendicular hasta el ángulo agudo

Sea ABΓ el triángulo acutángulo

Luego desde A se debe trazar una recta Δ.

Podemos notar que ΓB ha sido cortada al azar por Δ, esto hace que los cuadrados de ΓB y ΔB sean iguales a dos veces el rectángulo formado por ΓB y ΔB, además del cuadrado de ΔΓ.

ΓB + BΔ = 2 (ΓB y BΔ) + ΔΓ

Ahora añadamos a ambos ΓB y ΔB el cuadrado ΔA, entonces, los cuadrados ΓB, ΔB y ΔA son iguales a dos veces el rectángulo comprendido por ΓB y ΔB, y los cuadrados de AΔ y AΓ.

ΔA + ΓB + BΔ = 2 (ΓB y BΔ) + ΔΓ + ΔA

Por otro lado, tenemos que el cuadrado de AB es igual a los cuadrados de BΔ y ΔA porque el ángulo de Δ es recto. Ahora el cuadrado de AΓ es igual a los cuadrados de AΔ y ΔΓ. 

Aquí se reemplaza de la siguiente forma:

AB = BΔ + ΔA 
AG = AΔ + ΔΓ

Por lo tanto, los cuadrados de ΓB y BA son iguales al cuadrado de AΓ, y dos veces el rectángulo por ΓB y BΔ. 


Así, el cuadrado AΓ es menor que los cuadrados ΓB y BΔ en dos veces el rectángulo comprendido por ΓB y ΔB. 

Proposición 14:

Construir un cuadrado igual a una figura rectilínea dada

Sea A la figura rectilínea dada

Euclides se propone construir un cuadrado igual a la figura mostrada anteriormente. 

Para esto, construyamos un paralelogramo rectángulo BΔ, que sea igual a la figura rectilínea dada (A) que a su vez forme un rectángulo BΓΔE. 

Euclides dice que si BE es igual a EΔ se habrá hecho lo propuesto, pues así se construye la recta de la figura A. De lo contrario, entonces uno de los lados (BE o EΔ) tendría que ser mayor.

Supongamos que BE sea mayor y prolonguemos esta hasta un punto Z, y hágase Z igual a EΔ.

Luego dividamos BZ en dos partes iguales añadiendo un punto H en medio de la recta. 

Como podemos ver, junto con el punto H se forma también el punto Θ, que a su vez forma un semicírculo encima de la recta BZ. A consecuencia de esto formamos el semicírculo BΘZ.

El rectángulo comprendido por BE y EZ junto con el cuadrado EH son iguales al cuadrado HZ, debido a la misma proposición 5 de este libro. 

Sin embargo HZ es igual al cuadrado de HΘ, aunque también, los cuadrados de ΘE y EH son iguales al cuadrado HΘ. 

Por lo tanto, el rectángulo comprendido por BE y EZ junto con el cuadrado de EH son iguales a los cuadrados ΘE y EH.

Quítese de ambos (BE, EZ y ΘE) el cuadrado de HE y así quedaría que el ángulo comprendido por BE y EZ se igual al cuadrado EΘ.

Finalmente, el rectángulo comprendido por BE y EZ es BΔ porque EZ es igual a EΔ, por lo tanto, el paralelogramo BΔ es igual al cuadrado ΘE. Y como BΔ es la figura rectilínea dada(A), se puede construir un cuadrado EΘ igual a la recta dada A.

Conclusión

Al fin hemos terminado el libro II de Euclides que trata en su mayoría sobre los cuadrados y rectángulos que se pueden formar a partir de ciertas rectas. Se han añadido nuevos conceptos a conocer en esta etapa tales como el gnomon, que no había aparecido en el libro I, y que además nos ayudará a resolver las figuras geométricas sucesivas. Por supuesto, todo lo anteriormente nos preparará para completar el tercer libro relacionado con las circunferencias.

Este apunte ha sido logrado gracias Leila Reyes, quien corrigió y sugirió las modificaciones necesarias en este apunte. 

Euclides - Los Elementos (Libro I: Triángulos y conceptos básicos)

La vida de Euclides no es muy conocida y por lo tanto no hablaremos mucho de ella. Lo que sí nos dejó como legado es uno de los libros más difíciles de la Antigua Grecia, los ''Elementos''. Es uno de los tratados que deja casi obsoleto todos los tratados anteriores de geometría. Aristóteles usa mucho de los términos mencionados aquí para discutirlos filosóficamente en sus tratados de Física como de Metafísica. Esta vez veremos estos términos pero en función de las matemáticas.

Otros libros de Euclides:

Libro II: Cuadrados y rectángulos
Libro III: Circunferencias
Libro IV: Circunferencia inscrita y exinscrita de un triángulo




Referencias:

(1) El triángulo de esta proposición ha sido llamado el triángulo pitagórico porque representa el teorema de Pitágoras.

Definiciones:

(1) Unir dos rectas con una curva.

LOS ELEMENTOS

LIBRO I: TRIÁNGULOS Y CONCEPTOS BÁSICOS

Conceptos básicos

Antes de comenzar a ver las proposiciones de los triángulos debemos ver algunos conceptos básicos que Euclides utiliza. 

Ángulo Agudo: un ángulo que es menor a 90º

Ángulo recto: un ángulo que comprende exactamente 90º

Ángulo obtuso: un ángulo que comprende más de 90º pero menos de 180º.

Estos ángulos pueden encontrarse en todas las figuras geométricas que permitan tener tales medidas.

Tipos de triángulos

Así como también existen distintos tipos de ángulos, también existen distintos tipos de triángulos. Veamos los que se verán en las proposiciones sucesivas.

Triángulo equilátero (equiangulares): un triángulo donde cada uno de sus lados son congruentes entre sí, teniendo cada uno 60º.

Triángulo isósceles: un triángulo que tiene dos lados iguales así como también dos ángulos iguales. 

Triángulo escaleno: un triángulo que no tiene ninguno de sus lados iguales

Triángulo rectángulo: un triángulo que tiene un ángulo recto

Estos son al menos los triángulos a los que Euclides se refiere en las proposiciones.

Postulados

Euclides es conocido por aportar los 5 postulados propuestos en materia de figuras geométricas:

Postulado 1:

Una línea recta se hace estableciendo dos puntos 

Postulado 2:

Un segmento de la línea establecida puede extenderse infinitamente:

Postulado 3: 

Un radio puede extenderse desde un centro hasta cualquier punto de la circunferencia

Postulado 4:

Todos los ángulos rectos son iguales entre sí

Postulado 5:

Si una línea recta corta a dos rectas de modo que esta forme ángulos interiores menores a dos rectos (180º), dichas rectas se encontrarán. 

En efecto, si los ángulos hicieran 180º no se encontrarían y se extenderían indefinidamente como dos paralelas. 

Proposiciones de triángulos

Proposición 1:

Construcción del triángulo rectángulo sobre una recta

Euclides comienza la primera parte del Libro I construyendo un triángulo rectángulo sobre una recta dada, representada por A y B. Luego se conformará el triángulo añadiendo un punto Γ.

Ahora pondremos A como el centro de un círculo BΓΔ, mientras B será el centro del círculo AΓE. 

De este modo, AΓ es igual a AB porque A es el centro de ΔΓE y BΓ es igual a BA, así como ΓA es igual a ΓB. Por lo tanto, tenemos un triángulo equilatero, ya que AΓ, AB y ΓB son iguales. 

Proposición 2:

Poner un punto dado en una recta igual a otra recta dada

Ahora Euclides propone que desde un punto central se puedan construir dos rectas iguales. Para eso debemos construir el triángulo equilatero de la siguiente manera. 

Bajo este respecto, en el punto A hay que dibujar una recta igual al punto B.

Luego a al punto A dibujamos una línea para que forme el segmento AE. Después debemos hacer lo mismo con el punto B para formar el punto Z.

Ahora ocuparemos B como el centro de un círculo para conformar los puntos ΓHΘ. 

Si se fijan, al mismo tiempo son formados los puntos Λ y H. De igual manera, podremos decir en esta figura que BΓ es igual a BH. Sin embargo, aquí se encuentra un círculo aún más grande que ΓHΘ, que se forma a partir del centro Δ.

Así formamos la combinación de puntos HKΛ a partir del centro Δ del crículo. Aquí tenemos que AΛ es igual a BΓ el cual era el objetivo de esta proposición. 

Proposición 3:

Dos rectas desiguales; quitar de la mayor una recta igual a la menor

Esta proposición ya es un poco más fácil. Para lograr esto se debe comenzar con AB como una recta desigual, que a su vez será mayor a una recta Γ.

Recta Mayor:

Recta menor:

La idea es hacer que en AB se quite una recta igual a la recta Γ. Para eso, a partir de A deberemos formar una recta AΔ.

Luego de esto podemos formar un círculo con ΔE y Z.

De aquí sacamos que entre AB puede salir AE que es igual a Γ.

Proposición 4:

Dos triángulos tienen igual ángulo e igual recta, agregando un triángulo que se forme de manera subtendida. 

Figuremos dos triángulos completamente iguales: ABΓ y ΔEZ.

El triángulo subtendido(1) que se forme del primer triángulo será igual al triángulo subtendido que se pudiera formar en el segundo. 

Proposición 5:

Triángulos isósceles tienen las bases iguales entre sí

Supongamos un triángulo isósceles ABΓ que a sus puntos B y Γ se les prolongara una línea hasta llegar a los puntos Δ y E,  para formar el segmento BΔ y ΓE. 

Luego tomar al azar un punto Z en el segmento BΔ y un punto H en el segmento ΓE para luego formar una figura AZH. Desde aquí, la figura ZΓ será igual a la recta BH, lo que podría formar los triángulos AZΓ y ABH.

Por tanto, todos los triángulos que se formen desde la base serán iguales entre sí, por lo que eso quería demostrar la proposición. 

Proposición 6:

Los triángulos que estén subtendidos en los ángulos serán iguales entre sí

Tengamos un triángulo ABΓ y formemos con el punto Δ otro triángulo. ABΓ tiene todos sus lados iguales, de igual forma que con el triángulo ΔBΓ.

Sin embargo, ¿cómo puede ΔBΓ tener las mismas partes si ABΓ es mayor? Ciertamente dice Euclides que ΔΓ es igual a BΓ, pues imaginemos que ΔΓ subtendiera (bajara) a BΓ, sus proporciones serían las mismas. En conclusión, cuando los lados son iguales, también lo serán los ángulos que se subtienden.

Proposición 7:

No se levantarán sobre la misma recta dos rectas iguales.

Construyamos una recta AB que se conecten con un punto Γ y Δ. 

Por la proposición anterior podemos decir que AΓ es igual que AΔ, así como también lo son sus ángulos a partir de la combinación AΓΔ y AΔΓ. Así, el ángulo de AΔΓ es mayor que ΔΓB y este es menor que ΓΔB. Sin embargo, ΓB y ΔB son iguales, pero a la vez dijimos que ΔΓB es menor que ΓΔB lo cual es un absurdo. 

Por lo tanto, el único triángulo posible sería AΓB porque el otro sería mayor e igual a la vez. 

Proposición 8:

Si los tres lados de un triángulo son iguales a un triángulo de las mismas proporciones, entonces ambos triángulos son iguales en todos los respectos. 

Tengamos un ángulo ABΓ y otro ΔEZ

ABΓ y ΔEZ son iguales en sus lados, en sus ángulos y en sus bases, pero ¿qué pasa si ponemos un tercer triángulo que indicaremos con el punto H? Ese triángulo (como vimos en la proposición 7) no podría existir porque surgiría el problema de que es mayor por un ángulo y menor por el otro, por lo que solamente deberíamos poner un sólo triángulo. 

Proposición 9:

Dividir en dos partes un ángulo rectilíneo

Dibujemos un ángulo rectilíneo BAΓ

Este triángulo ha sido dividido por la recta AZ la cual se llama bisectriz, lo que hace que ΔAZ y EAZ sean totalmente iguales al ser estos dos partes de un mismo triángulo (BAΓ). 

Proposición 10:

Dividir en dos partes iguales una recta finita

Ahora construyamos un triángulo equilátero con una base AB y un punto superior Γ.

La bisectriz ΓΔ ha dividido el triángulo equilátero AΓB cuyas partes AΔΓ y BΔΓ son exactamente iguales. En otras palabras, se ha podido separar el triángulo equilátero AΓB  a partir de la bisectriz ΓΔ.

Proposición 11:

Trazar una línea que forme dos ángulos rectos en un triángulo equilátero. 

Prolonguemos una recta AB por debajo de un triángulo equilátero ΔZE y tracemos una bisectriz ZΓ.

Lo que se quiere probar aquí es que de ZΓ se pueden generar dos ángulos rectos con la base AB siendo Γ el punto dado.

Proposición 12:

Trazar una recta perpendicular en una recta infinita que forme ángulos rectos desde un punto que no está en ella

La recta infinita será AB, mientras que la perpendicular será ΓΘ que esté trazando la recta infinita para formar los ángulos rectos. 

Luego pongamos a Γ como el centro de un círculo, para luego agregar los puntos HE que serán los puntos del triángulo.

Así, el triángulo HΘΓ son iguales al triángulo EΘΓ lo que nos dice que es posible trazar una recta perpendicular como ΓΘ, desde un punto que no pertenecía a AB como Γ.

Proposición 13:

Una recta levantada sobre otra recta puede formar dos rectos, o dos ángulos. 

Formamos una recta ΓΔ y sobre esta añadimos una recta AB, siendo ΓBΔ y ABΔ dos rectos. 

Ahora, si queremos buscar los dos ángulos rectos, entonces deberíamos trazar EB para formar una recta que nos de dos ángulos rectos.

Así, tenemos que EB forman los dos ángulos rectos, mientras que AB forman dos rectos que es lo que se quería demostrar. 

Proposición 14:

Si dos rectas forma un punto adyacente, ambas estarán en línea recta.

Formen ABΓ un ángulo adyacente con ABΔ que sería iguales a dos rectos. 

Estos dos ángulos formarían 180 grados, pero veamos si se puede formar aún otra recta a partir de la imagen. 

En esta imagen tenemos que ΓBA con ABE no forman los 180 grados, puesto que si lo hicieran ABE y ABΔ serían iguales, lo cual no es posible porque ABΔ es mayor. Por lo tanto, no podría existir una recta igual a BD.

Proposición 15:

Si dos rectas se cortan, hacen los ángulos del vértice iguales entre sí.

Se debe trazar una recta ΔΓ con otra AB que tengan un punto E.

Los ángulos ΓEA y AEΔ son iguales a dos rectos (proposición 13), al igual que las rectas AEΔ y ΔEB que también son iguales a dos rectos. 

Miremoslo bajo la siguiente imágen:

En estas, Alfa con Gamma hacen los 180 grados justo como lo vimos en la proposición anterior. Con esto podemos concluir, que los ángulos opuestos por el vértice, como lo son Alfa y Beta, siempre serán iguales. 

Proposición 16:

Si a un triángulo se le prolonga uno de sus lados, el ángulo externo será mayor a los internos

Téngase un triángulo ABΓ y prolongamos la recta BΓ hasta Δ. 

Euclides dice que los ángulos de AΓΔ son mayores a los de ΓBA y BAΓ. En efecto, AΓΔ representaría un ángulo obtuso, mientras que los ángulos internos serían sólo agudos. 

Luego dividamos ABΓ a partir de una recta creada por BE y que se prolongue hasta Z. Finalmente, desde Z se debe trazar una línea hasta Γ.

Luego prolonguemos Γ para formar la recta ΓH.

Bajo este respecto, el triángulo BAE es igual al triángulo ZEΓ, al igual que también son iguales sus ángulos. Por otro lado, también debemos decir que EΓΔ como AΓΔ es mayor que BAE. 

De este modo, cualquier triángulo que sea prolongado por uno de sus lados, el ángulo externo que se forme será mayor que cada uno de los ángulos internos. 

Proposición 17:

Los ángulos de todo triángulo son menores que dos ángulos rectos.

Tengamos un triángulo ABΓ y cuyos ángulos son menores que dos rectos. Luego prolonguemos BΓ hasta Δ, para que de este modo el ángulo AΓΔ es mayor que los ángulos internos ABΓ, excepto por el ángulo AΓB el cual junto con AΓΔ forman dos rectos, aunque AΓΔ sigue siendo el mayor de los ángulos anteriores. 

Así ABΓ, BΓA y BAΓ son menores el ángulo AΓΔ que es externo y es lo que se quería demostrar.

Proposición 18:

En un triángulo dado, el lado mayor subtiende al ángulo mayor.

Tenemos entonces un ángulo ABΓ que es mayor que el ángulo BΓA. 

Luego trazar una bisectriz desde B para formar el punto Δ.

AΔB es un ángulo externo al triángulo BΓΔ y mayor que el ángulo ΔΓB (proposición 16).

Ahora AΔB es igual al ángulo ABΔ porque el lado AB es igual al lado AΔ (lo que formaría un triángulo isósceles). 

Por lo tanto, como ABΔ es mayor que AΓB, ABΓ sería mucho mayor ΔΓB por lo que la recta AΓ sería mayor a la recta AB. 

Proposición 19:

En todo triángulo, el ángulo mayor subtiende al lado mayor.

Tengamos un triángulo ABΓ teniendo su ángulo ABΓ mayor que el BΓA. 

Por supuesto AΓ es mayor que el lado AB por lo que se puede demostrar que el ángulo mayor (AΓB) subtiende al lado mayor (AΓ) que es lo que se quería demostrar.

Proposición 20:

En un triángulo, los dos lados de este tomados juntos son mayores que el restante. 

Tengamos nuevamente un triángulo ABΓ de la siguiente forma.

Luego debemos prolongar la recta BA hasta llegar a un punto Δ para luego unir este con Γ.

ΔA es igual a AΓ y AΔΓ es igual a AΓΔ, y BΓΔ es mayor que AΓΔ y que AΔΓ. Luego, como el ángulo mayor es subtendido BΔ será mayor que AΓ, y AΔ es igual a AΓ.

Finalmente BA y AΓ tomados juntos son mayores que BΓ que es el lado restante y es lo que se quería demostrar. 

Proposición 21:

A partir de los extremos de un triángulo se construyen dos rectas que se encuentran en el interior del triángulo, las rectas construidas son menores que los lados del triángulo, pero tienen un ángulo mayor.

Construyamos un triángulo ABΓ. 

Dentro del triángulo fórmese B con Δ y Γ con Δ dentro del mismo triángulo. 

Luego prolongar la recta BΔ hasta formar el punto E sin salir del triángulo. 

Debemos recordar la proposición 16 donde el ángulo externo es mayor que el interno. 

En el triángulo ΓEΔ su ángulo externo que sería BΔΓ es mayor que el ángulo ΓEΔ (BΔΓ>ΓEΔ). 

De la misma forma, siguiendo la misma proposición 16, tendremos que decir que BAE es menor que su ángulo externo ΓEΔ (ΓEΔ>ABE). 

Finalmente, BΔΓ es mucho mayor que BAΓ, porque BAΓ es mucho menor que ΓEB. (BΔΓ>ΓΔE>ABE).

Así, BΔΓ es menor en cuanto a los lados del triángulo, pero es mucho mayor en cuanto al ángulo que tiene. 

Proposición 22:

Construir un triángulo con tres rectas que son iguales a otras tres rectas. 

Tengamos tres rectas dadas 

A____________
B__________
Γ________

Ahora, hagámos que la unión de 2 de ellas sean mayor que la restante; por ejemplo, uniéndose A y B son mayores que Γ, al igual que AΓ serían mayores que B y finalmente B y Γ mayores que A.

AB>Γ
AΓ>B
BΓ>A

Ahora debemos construir un triángulo con esas rectas dadas. 

Primero pongamos una recta ΔE

Luego pongamos un punto Z que representará la recta dada A (ΔZ) que propusimos anteriormente. 

Luego pongamos un punto H (ZH) que representará la recta dada B y un punto Θ el cual representará con H el punto Γ(ΘH). 

Tomando la Z como centro, dibujemos una especie de círculo que llegue hasta Δ y terminar el círculo con Λ.

Finalmente, hágase otro círculo teniendo como centro H y poniendo arriba K, siendo Θ el extremo de este círculo. Luego tendremos el círculo KΛΘ y trásence KZ y KH.

Euclides dice que se ha construído un triángulo (KZH) a partir de las rectas dadas A, B y Γ.

Z es el centro del círculo, ZΔ es igual a ZK y así ZΔ y ZK son iguales a la recta dada A (ZΔ; ZK = A).

H es el centro del círculo ΛKΘ, HΘ es igual a HK y así HΘ y HK representan a la recta dada Γ. (HΘ; HK =Γ).

ZH era igual a la recta dada B y finalmente: KZ, ZH y HK son iguales a las rectas dadas A, B y Γ.

Así, es perfectamente posible construir un triángulo con rectas dadas. 

Proposición 23:

Hacer un ángulo recto igual a otro ángulo recto dado, sobre una recta dada.

Tengamos una recta dada AB y sea A uno de sus puntos. 

Luego tengamos un ángulo recto dado:

Lo que se propone hacer Euclides es dibujar un ángulo rectilíneo igual a la recta dada AB.

Tomemos las rectas ΓΔ, ΔE y ΓE para luego construir el triángulo AZH. 

Así se hizo un ángulo recto dado sobre otro ángulo recto dado. 

Proposición 24:


Dos triángulos tienen sus dos lados respectivamente iguales, pero si uno tiene un ángulo comprendido por las rectas mayor que el otro, su base también será mayor

Tengamos dos triángulos ABΓ (teniendo sus lados AB y AΓ iguales) y ΔEZ (siendo ΔE y ΔZ iguales). 

AB = ΔE
AΓ = ΔZ

Hay que añadir que la base ΓB es mayor que la base EZ

El punto EΔH es igual al ángulo BAΓ. En ese respecto, hágase ΔH igual a ambas rectas AΓ y ΔZ. Luego hágase EH y ZH. 

Bajo este respecto:

AB = ΔE
AΓ = ΔH

El ángulo BAΓ es igual al ángulo EΔH y si es así la base ΓB es igual a EH. Por otro lado, ΔZ es igual a ΔH y así, el ángulo ΔHZ es igual al ángulo ΔZH, este es mayor que EHZ y éste menor que EZH. De esta forma, el lado EH es mayor que el lado EZ 


BAΓ = EΔH
ΓB = EH

ΔHZ = ΔZH
ΔZ = ΔH

ΔZH > EHZ
EHZ < EZH

Ahora, EH es igual a BΓ que es mayor a EZ, lo que quiere decir que EH y BΓ son las bases mayores del ángulo comprendido HZE. 

Proposición 25:

Dos triángulos tienen dos lados iguales entre sí, pero uno tiene una base mayor que el otra. Si es así, sus ángulos también serán mayores. 

Tengamos dos triángulos ABΓ y ΔEZ que tienen sus lados AB y AΓ iguales a ΔE y ΔZ.

La conclusión de esta proposición es bastante fácil, pues si la base de un triángulo es mayor que otro triángulo, sus ángulos también son mayores. Está claro que la base BΓ est mucho mayor a EZ.

Proposición 26:

Si dos triángulos tienen dos ángulos y un lado de uno iguales a los de otros, los lados y el ángulo restantes también serán iguales. 

Tengamos los triángulos ABΓ y ΔEZ 

Sus ángulos son iguales es decir:

ABΓ y ΔEZ = BΓA y EZΔ

Sus bases también son iguales en sentido de que BΓ y EZ son iguales.

Sus lados también serán iguales:

AB = ΔE
AΓ = ΔZ

Para comprobar todo esto, hágase en AB un punto H que se trace hasta Γ.

Pretendamos que BH sea igual a ΔE, y BΓ a EZ. Así, de este modo tendríamos que BHΓ sea igual a EΔZ considerando que BH es igual a ΔE. 

BH = ΔE
BΓ = EZ

Sin embargo, el ángulo ΔZE es igual que BΓA por lo cual BΓH sería igual al ángulo BΓA, lo cual es absurdo. 

Así, BH no es igual a ΔE, aunque BΓ es igual a EZ lo que resultaría en que AΓ es igual a ΔZ. 

Si se duda de que BΓ sea igual a EZ, entonces imagínese que el uno sea mayor que el otro.

Si BΘ es igual a EZ y AB a ΔE, entonces los dos lados AB y BΘ son iguales. Así, el triángulo ABΘ es igual al triángulo ΔEZ así como también el ángulo BΘA es igual a EZΔ; sin embargo, EZΔ es igual a BΓA. 

El ángulo externo de AΘΓ sería BΘA, en este sentido, sería igual a BΓA lo cual es absurdo. 

Finalmente, si dos triángulos tienen dos ángulos y un lado de uno iguales a los de otros, los lados y el ángulo restantes también serán iguales. 

Proposición 27:

Si una recta hace ángulos externos iguales entre sí, las dos rectas serán paralelas entre sí

Tengamos dos rectas respectivamente AB y ΓΔ:

A estas dos rectas se debe hacer un trazo de EZ entre los puntos AB y entre los puntos ΓΔ.

Así se formarán los ángulos AEZ y EZΔ que son iguales entre sí. 

Luego deberemos prolongar AB y ΓΔ para que se construya un punto H. 

A partir del punto H formaremos el ángulo EZH y si éste ángulo uniera las paralelas entonces deberíamos decir que AEZ es igual a EZH, lo cual es imposible, porque es EZΔ es igual a AEZ. Por otro lado, EZH es menor a EZD.

Finalmente AB es totalmente paralela a ΓΔ lo cual está hecho por la recta EZ y no por H. 

Proposición 28:

Si una recta incide sobre dos rectas y al mismo tiempo hace que los ángulos internos y externos sean iguales, entonces las dos rectas serán paralelas entre sí. 

Utilicemos las mismas rectas AB y ΓΔ de la proposición anterior:

Luego pongamos una recta entre medio de ellas que sea EZ y que al mismo tiempo forme los puntos H y Θ.

De este modo, EHB será igual que HΘΔ.

Teniendo esas proposiciones, veamos el otro lado de la recta. 

Si EHB es igual a HΘΔ, entonces AHΘ será igual a HΘΔ también, lo que hace que AB y ΓΔ sean paralelas. 

Proposición 29

Si tenemos dos rectas paralelas trazadas por una recta vertical, esta hará que tanto los ángulos externos e internos de los dos lados sean iguales.  

Utilicemos la misma imágen y los puntos de la proposición 28

Si AHΘ es igual a HΘΔ, el ángulo externo EHB es igual al ángulo interno HΘΔ. 

Ahora, veamos qué pasa si uno de estos puntos fuera mayor que el otro. Si AHΘ fuera mayor que el ángulo HΘΔ, entonces las rectas que se suponían paralelas (AB y ΓΔ) se encontrarían, lo cual es absurdo pues las paralelas no se encuentran (postulado 5 de Euclides).

Proposición 30:

Las paralelas a una misma recta son iguales entre sí

Tengamos tres rectas: AB, EZ y ΓΔ. 

Luego trace una línea HK que a su vez forme un punto intermedio Θ. 

Bajo este respecto, el ángulo AHK será igual a HΘZ y también igual al ángulo HKΔ, así como también AHK también es igual a HKΔ, lo que prueba que las tres rectas AB, EZ y ΓΔ son paralelas entre sí. 

Proposición 31:

Trazar una línea recta desde un punto dado hasta la siguiente recta dada

Tengamos dos rectas BΓ y EZ dadas que se unan por una línea recta paralela AΔ. 

Los ángulos EAΔ serán iguales a AΔΓ (que por si no lo notaron forma una especie de ''Z''). Por lo demás, sea AZ el resultado de prolongar EA. 

La incidencia de AΔ ha hecho que EAΔ y AΔΓ tengan ángulos alternos iguales, lo que además hace paralelas a EZ y BΓ.

Así se ha hecho desde un punto dado AΔ para que las dos rectas adicionales sean paralelas. 

Proposición 32:

Si un lado del triángulo se prolonga, el ángulos externo es igual a los dos ángulos internos.

Tengamos un triángulo ABΓ

Prolonguese BΓ hasta Δ

Euclides dice que el triángulo AΓΔ es igual a los ángulos internos ABΓ y ΓAB. Además, dice que ABΓ, BΓA y ΓAB son iguales a dos rectos. 

Para probar que esto es cierto, Euclides pide al lector que se trace una línea con punto E paralelo a la línea AB.

Aquí tenemos que BAΓ y AΓE son iguales entre sí, así como también EΓΔ es igual a ABΓ. Y como AΓΔ es igual a BAΓ, entonces AΓΔ,  BAΓ y ABΓ son iguales. 

El ángulo AΓΔ se le añade el ángulo AΓB que juntos equivalen a 180 grados (dos rectos). De esta manera, el ángulo externo será igual a los ángulos opuestos e internos, y que los ángulos interiores del triángulo forman 180º.

Proposición 33:

Las rectas que se unen por los extremos son iguales y paralelas

Tengamos rectas BA y ΓΔ que se unan creando sus propias rectas AΓ y BΔ, y finalmente tracese BΓ.

Todas las rectas que vemos aquí se unen entre sí para formar un paralelogramo. Tenemos dos paralelas que se unen con otra a través de las rectas:

AB = ΓΔ (siendo BΓ común a las dos)
AB y BΓ = BΓ y ΓΔ
ABΓ = BΓΔ
AΓ = BΔ

Finalmente, es la recta BΓ la que hace iguales y paralelas a las rectas AΓ y BΔ.

Proposición 34:

Las áreas de un paralelogramo son iguales entre sí, mientras que una diagonal divide el área en dos partes iguales

Tengamos AΓΔB como el área del paralelogramo

Las partes de AΓΔB son todas iguales además de que BΓ divide el área en dos partes iguales. ABΓ y ΓBΔ serían partes iguales de la misma área del paralelogramo. 

Es decir, la diagonal divide el paralelogramo en dos partes iguales.

Proposición 35:

Los paralelos que están sobre la misma base y entre las mismas paralelas son iguales entre sí

Tengamos un paralelogramo ABΓΔ

Luego unase con un paralelogramo EBΓZ y fórmese un punto H entre los dos paralelogramos de la siguiente forma:

Estos dos paralelogramos comparten las mismas rectas paralelas que serían AZ y BΓ. De acuerdo con Euclides, los dos paralelogramos son iguales. 

AΔ sería igual a BΓ ya que estas son las dos paralelas de las que habíamos hablado. Del mismo modo, BΓ es igual a EZ, así como también AΔ es igual a EZ. 

Por otro lado, AE es igual a ΔZ, así como AB es igual a ΔΓ. 

En cuanto a los triángulos, EAB es igual a ΔZΓ y quítese el triángulo ΔHE para formar el trapecio ABHΔ, que a su vez es igual al paralelogramo EHΓZ.

Así, los paralelogramos ABΓΔ y EBΓZ que comparten la misma base son iguales entre sí. 

Proposición 36:

Los paralelogramos que están sobre bases iguales y entre las mismas paralelas son iguales entre sí

Tengamos ABΓΔ y EZHΘ como paralelogramos que están sobre una base BΓ y ZH entre las paralelas AΘ y BH.

Unase B con E y Γ con Θ.

BΓ es igual a EΘ y ZH, por lo que podríamos decir que EBΓΘ es otro un paralelogramo que también es igual a ABΓΔ, pues tienen la misma base. 

Así, los paralelogramos que tienen las bases iguales (ABΓΔ y EZHΘ) y están entre las mismas paralelas (EBΓΘ) son iguales. 

Proposición 37:

Los triángulos que están en la misma base y entre las mismas paralelas son iguales entre sí

Tengamos los triángulos ABΓ y ΔBΓ que están sobre la misma base BΓ y entre las mismas paralelas AΔ y BΓ.

Ahora debemos prolongar AΔ hasta Z y ΔA hasta E, para luego unir cada lado con B y Γ.

     
Así tenemos dos paralelogramos que son EBΓA y ΔBΓZ y que comparten la misma base BΓ y EZ. 

ABΓ sería la mitad del paralelogramo EBΓA, ya que AB lo divide en dos partes iguales (como la proposición 34 lo demostraba). ΔBΓ sería la mitad de ΔBΓZ que es dividida por ΔΓ. Así, ABΓ y ΔBΓ son iguales que es lo que se quería demostrar. 

Proposición 38:

Los triángulos que están sobre las mismas bases y entre las mismas paralelas son iguales entre sí. 

Pareciera ser que es igual a la proposición 37, pero la verdad es que esta se diferencia porque son más de una base las que se comparan. 

Tengamos ABΓ y ΔEZ como los triángulos que comparten una base  BΓ y EZ y entre las mismas paralelas BZ y ΔA.

Como ABΓ y ΔEZ tienen la misma base, también serán iguales. 

Prolonguemos AΔ hasta H y hasta Θ. 

Así, HBΓA y ΔEZΘ son paralelogramos que son iguales porque están sobre las bases iguales BΓ y EZ.  ABΓ representa la mitad de HBΓA así como ZEΔ representa la mitad de ΔEZΘ. 

De este modo, las bases BΓ y EZ dan la igualdad a los triángulos que están en los paralelogramos. 

Proposición 39:

Los triángulos iguales que están sobre la misma base y en el mismo lado, están en las mismas paralelas. 

Tengamos ABΓ y ΔBΓ triángulos iguales que están sobre una misma base BΓ. Tracemos AΔ para que BΓ y AΔ sean paralelas.

Desde el punto A trazar una recta hasta el punto E y de ahí hasta Γ.

El triángulo ABΓ sería igual al triángulo EBΓ porque está sobre la misma base BΓ.  Ahora, ABΓ es igual a ΔBΓ y así tendríamos que decir que ΔBΓ también es igual a EBΓ, pero como sabemos, esto es imposible porque no pueden ser los dos iguales siendo que EBΓ claramente es menor que ΔBΓ. Así tenemos que AE no es paralela a BΓ y en realidad ninguna otra lo es porque la única paralela a BΓ es AΔ. 

Proposición 40:

Los triángulos iguales que están sobre bases iguales y en el mismo lado, están también entre las mismas paralelas

Tengamos dos triángulos: ABΓ y ΓΔE que están sobre las mismas bases BΓ y ΓE. Por lo tanto, BE es paralela a AΔ.

Como podemos ver en la figura, se traza AZ para hacer una especie de paralela a BE. Euclides dice primeramente que el triángulo ABΓ es igual al triángulo ZΓE porque están sobre las mismas bases BΓ  y ΓE. 

Sin embargo, en ese caso tendríamos que decir que ΔΓE tendría que ser igual que ABΓ, pues también tienen la misma base, por lo que se produciría un error porque ZΓE también es igual a ABΓ lo que es absurdo. 

Así AZ no es paralela a BE por lo que se sacaría como conclusión que los triángulos iguales que está sobre bases iguales y en el mismo lado, están en las mismas paralelas. 

Proposición 41:

Si un paralelogramo tiene la misma base que un triángulo y está en las mismas paralelas, el paralelogramo es el doble del triángulo

Tengamos el paralelogramo ABΓΔ teniendo una base BΓ que la comparte con EBΓ. Al mismo tiempo, estas tienen que estar entre las paralelas BΓ y AE.

Digamos que el triángulo ABΓ es igual al triángulo EBΓ porque están sobre la misma base (BΓ) y entre las mismas paralelas (AE y BΓ). 

El paralelogramo ABΓΔ es el doble que ABΓ porque la recta AΓ lo divide en dos partes iguales (recuérdese la proposición 34). Así el paralelogramo ABΓΔ que tiene la misma base que ABΓ que es igual a EBΓ, y EBΓ sería la mitad del paralelogramo.

Proposición 42:

Hacer un ángulo rectilíneo dado en un paralelogramo igual a un triángulo dado. 

Tengamos ABΓ como el triángulo dado y Δ el ángulo rectilíneo dado. 

Y el ángulo dado

Se divide BΓ por la mitad con el punto E. El ángulo ΓEZ debe ser igual al ángulo planteado que dijimos sería Δ. 

ZEΓH es el paralelogramo que es el doble de AEΓ porque tienen la misma base que sería EΓ, además de estar en las mismas paralelas. 

ZEΓH sería igual al triángulo ABΓ porque estos dos son el doble de AEΓ. 

Finalmente en el paralelogramo ZEΓH tenemos el único ángulo rectilíneo que en este caso sería ΓEZ, el cuál es el ángulo dado Δ.

Proposición 43:

En todo paralelogramo, los complementos del mismo situados en la diagonal son iguales entre sí. 

Tengamos ABΓΔ el paralelogramo y sea AΓ su diagonal.

Tengamos además EΘ y ZH otros paralelogramos en torno a AΓ.

Sean los complementos BK y KΔ que asu vez son iguales.

ABΓ es igual al triángulo AΓΔ, así como también AEK es igual a AΘK. 

KZΓ es igual al triángulo KHΓ, así como este último también es igual a AEK como KZΓ es igual a AΘK. 

En ese respecto BK es igual a KΔ y estos mismos serían los complementarios. Por lo tanto, queda probado que los complementos (BK y KΔ) que se encuentran en la diagonal (AΓ) son iguales entre sí. 

Proposición 44:

Aplicar a una recta dada en un ángulo rectilíneo dado, un paralelogramo igual a un triángulo dado

Primero tengamos el triángulo dado Γ y el ángulo dado Δ

Ahora construyamos un paralelogramo BEZH el cual tiene que tener en su interior el triángulo Γ, específicamente en el ángulo EBH que sería igual al ángulo dado Δ.

Prolongar AB hasta E y prolongar ZH hasta Θ, y que ésta se una con A. Finalmente tracese ΘB.

Prolonguese la línea ΘB hasta llegar a un punto K que una la recta ZE (Proposición 27). Ahora, hágase una recta KΛ para que esta sea paralela con EA y ZΘ. 

En este respecto, AΘZ y ΘZE son iguales a dos rectos, mientras que los ángulos BΘH y HZE son menores que dos rectos debido a que BΘH representa un ángulo menor a un recto. Así BΘH (ángulo agudo) y HZE (ángulo recto) no alcanzan a hacer dos rectos (180º).

ZΛKΘ sería un paralelogramo y ΘK su diagonal. Luego prolonguese H hasta llegar a un punto M entre la recta KΛ. 

ΛB y BZ son los complementos del paralelogramos más grande. Por otro lado, si el triángulo Γ es igual a BZ, entonces ΛB también tendrá el triángulo Γ en su interior. 

El ángulo HBE (donde está contenido Δ) es igual al ángulo ABM y si esto es así, entonces el ángulo Δ también está contenido BΛ. Recordemos que la demostración para introducir un ángulo dado aparece en la proposición 42.

Proposición 45:

Construir en un ángulo rectilíneo dado un paralelogramo igual a una figura rectilínea dada. 

Tengamos ABΓΔ la figura rectilínea dada y E el ángulo rectilíneo dado.

La idea es que en el ángulo dado E se construya un paralelogramo igual a ABΓΔ. 

Construyamos un ángulo ΘKZ que representará al ángulo dado E, que a su vez será igual a ABΔ.

Luego hay que añadir un punto H que coincida con Θ. 

Después debemos hacer otro ángulo que sea igual al paralelogramo dado que era ABΓΔ, pero sólo ocuparemos el ángulo ABΓ usando HΘM que será igual al ángulo E. Finalmente, formemos el punto Λ para terminar de formar el paralelogramo. 

Así, tendríamos los siguientes ángulos que coinciden con E. 

E = HΘM, ΘKZ, ZKΘ, KΘH

También ΘHZ y MΘH (que formarían una Z) son iguales a ΘHΛ, dando así cada uno una combinación de dos rectos (180 grados).

De este modo, KZΛM formaría un paralelogramo. 

Luego, como ABΔ del triángulo dado es igual al paralelogramo ZΘ y el triángulo ABΓ es igual al paralelogramo HM, entonces tenemos que ABΓΔ es igual a KZΛM. 

Proposición 46:

Trazar un cuadrado a partir de una recta dada

Tengamos una recta dada AB por el cual se debe construir el cuadrado. 

Prolonguese A hasta Δ, pero hacia arriba de modo de construir uno de los lados del cuadrado y finalmente para terminar la totalidad del cuadrado se prolonba .

Luego en BA prolonguese hasta el punto Γ. 

AΔEB sería un paralelogramo que tiene todas sus rectas iguales, lo cual lo hace un paralelogramo equilátero. 

Por lo tanto,un cuadrado se pudo construir a partir de la recta dada AB.

Proposición 47(1):

En un triángulo rectángulo, el cuadrado del lado que subtiende al ángulo recto es igual a los cuadrados de los otros lados del ángulo recto

Tengamos por ABΓ como el triángulo rectángulo en el cual su ángulo recto es BAΓ.

A partir de BAΓ hágase el cuadrado BDEΓ.

Luego, a partir de BA debe construirse el cuadrado HB y en AΓ el cuadrado ΘΓ.

Como podemos ver H está en línea recta con AΓ, así como BA está en línea recta con AΘ. 

El ángulo ΔBΓ es igual al ángulo ZBA porque los dos son ángulos rectos, así como ΔBA es igual a ZBΓ. 

Todos los cuadrados que se forman a partir ΔBΓ son iguales, pues la base de BΓ es igual al cuadrado HB y el cuadrado ΘΓ. De este modo, el cuadrado de BΓ (BDEΓ) sería igual a los cuadrados AB y AΓ juntos. 

Proposición 48:

Si en un triángulo el cuadrado de uno de los lados es igual a los cuadrados de los dos lados restantes del triángulo, el ángulo comprendido por esos ángulos restantes del triángulo es recto

Tengamos un ángulo recto BAΓ, y luego prolonguese BA hasta llegar al punto Δ para formar otro ángulo recto. 

Los cuadrados que se formen de ΔA y AB son iguales, así como también es igual el cuadrado de ΔΓ y ΓB, lo que hace que ΔAΓ y BAΓ sean iguales. Por lo tanto, tenemos que un triángulo ΔΓB el cuadrado de uno de sus lados restantes (ΓB o ΓΔ) será igual al cuadrado de los lados restantes los cuales comprenderá un ángulo recto. 

Conclusión

¿Cuál es la importancia de Euclides en la historia de las matemáticas y del pensamiento en general? sus libros se utilizaron como textos de estudio para entender los axiomas que tienen las figuras geométricas. Aún en nuestro siglo los axiomas de Euclides siguen teniendo vigencia en el sistema escolar, así como también en los más complejos estudios de las matemáticas. Es cierto que muchas cosas de Euclides se han modificado; como por ejemplo, el último postulado del cual otros matemáticos han aportado muchas otras cosas. No obstante, no podemos desconocer que los inicios de dichas modificaciones no hubieran sido posibles sin Euclides.

Este apunte ha sido logrado gracias Leila Reyes, quien corrigió y sugirió las modificaciones necesarias en este apunte.